Bryły platońskie
Wielościany foremne to bryły, których wszystkie ściany są przystającymi wielokątami foremnymi i w których z każdego wierzchołka wychodzi tyle samo krawędzi.
Dla Platona bryły te miały zasadnicze znaczenie, uznawał bowiem, że materia zbudowana jest z całostek i nie jest podzielna, a całostki te mają charakter idealny. Nie są bowiem ciałami stałymi, lecz figurami geometrycznymi. Idealną najprostszą figurą geometryczną jest trójkąt, czyli płaszczyzna ograniczona najmniejszą liczbą linii prostych. Według Platona trójkąty są najprostszym elementem budulcowym, podstawową cegiełką, z której zbudowany się Kosmos.
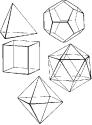Z trójkątów równobocznych złożyć można trzy bryły idealne - tetraedr
(czworościan foremny), oktaedr (ośmiościan foremny), ikosaedr
(dwudziestościan foremny).
Bryły te, według Platona, odpowiadają trzem elementom (ogień, powietrze, woda).
Czwarty element - ziemię, reprezentuje heksaedr (sześcian), którego każda
ściana da się podzielić na dwa trójkąty, jest więc też zbudowany z trójkątów.
Istnieje wreszcie piąta bryła foremna - dodekaedr,
zbudowana z 12 pięciokątów regularnych, którą Platon uznał za zespolenie całości,
bryłę łączącą wszystkie elementy.
Te wielościany to tzw. bryły platońskie, będące wyczerpującym zestawem wielościanów foremnych. Uznał, że cała rzeczywistość jest zorganizowana jako odbicie owych podstawowych figur geometrycznych, czyli form najdoskonalszych.
Dlaczego tylko pięć brył?
Pitagoras udowodnił, że płaszczyzna dookoła punktu może być zapełniona jednolicie
tylko trzema rodzajami wielokątów foremnych: trójkątami, kwadratami albo
pięciokątami. Żeby powstało naroże potrzebne są co najmniej trzy ściany oraz suma
kątów płaskich w wierzchołku musi być mniejsza od kata pełnego. Wszystkie
ściany w przypadku brył platońskich są jednakowe. Zatem jeśli wielokąty foremne
tego samego rodzaju maja utworzyć naroże, to takich kombinacji jest właśnie pięć.
