Przestrzeń. Dopełnienie zbioru
Często w algebrze zbiorów mamy do czynienia ze zbiorami, które są podzbiorami pewnego ustalonego zbioru, który nazywamy przestrzenią
Nich X będzie przestrzenią.
Dopełnieinem zbioru A ⊂ X nazywamy zbiór X\A i oznaczamy
symbolem A'
A' jest zatem zbiorem tych wszystkich elementów przestrzeni X, które nie są elementami zbioru A. Jeżeli przestrzeń X jest ustalona, to z definicji dopełnienia zbioru wynika, że dla każdego A ⊂ X i każdego x∈X spełniony jest warunek (x∈A') ⇔ (x∉A).
Dopełnienie zbioru A' można przedstawić graficznie jako obszar zacieniowany:
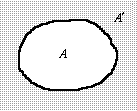
Dla dowolnego podzbioru A przestrzeni X zachodzi:
X ∪ A = X
X ∩ A = A
X' = 0
0' = X
(A')' = A