logowanie

Działania na wektorach

Suma wektorów

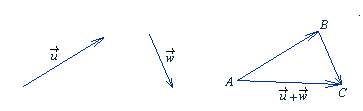
Aby dodać do siebie dwa wektory ${\displaystyle \overrightarrow{u}\text{ i }\overrightarrow{w}}$, należy obrać sobie dowolny punkt. W punkcie A zaczepiamy początek wektora równego wektorowi ${\displaystyle \overrightarrow{u}}$. Jego koniec znajduje się w punkcie B. W punkcie B umieszczamy początek wektora równego wektorowi ${\displaystyle \overrightarrow{w}}$. Jego koniec znajduje się w punkcie C. Wektor ${\displaystyle \overrightarrow{AC}}$ równy jest wektorowi ${\displaystyle \overrightarrow{v}=\overrightarrow{u}+\overrightarrow{w}}$.

Wektorami składowymi danego wektora nazywa się wektory, których suma jest równa danemu wektorowi. Wektor będący sumą kilku wektorów nazywany jest wektorem wypadkowym.

Różnica wektorów

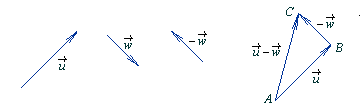
Różnicą wektorów ${\displaystyle \overrightarrow{u}\text{ i }\overrightarrow{w}}$ nazywamy sumę wektorów ${\displaystyle \overrightarrow{u}}$ i przeciwnego do ${\displaystyle \overrightarrow{w}}$.
${\displaystyle \overrightarrow{v}=\overrightarrow{u}-\overrightarrow{w}}=\overrightarrow{u}+(-\overrightarrow{w})$

Mnożenie wektora przez liczbę (skalar)
Iloczyn danego wektora ${\displaystyle \overrightarrow{u}}$ przez skalar s, to wektor ${\displaystyle \overrightarrow{v}}=s·{\displaystyle \overrightarrow{u}}$ o tym samym kierunku, ale długości stanowiącej iloczyn długości wektora przez wartość skalara s i zwrocie zgodnym ze zwrotem wektora jeśli s > 0 i przeciwnym gdy s < 0.

Iloczynem dowolnego wektora i liczby s = 0 jest wektor zerowy, a także iloczynem wektora zerowego i dowolnej liczby jest wektor zerowy.

Tak określone mnożenie spełnia podstawowe własności algebraiczne - jest łączne i rozdzielne.

Działania na płaszczyźnie

Jeżeli ${\displaystyle \overrightarrow{u}}=\text{ i }{\displaystyle \overrightarrow{w}}=$, to
${\displaystyle \overrightarrow{u}}+{\displaystyle \overrightarrow{w}}=$
${\displaystyle \overrightarrow{u}}-{\displaystyle \overrightarrow{w}}=$

Jeżeli ${\displaystyle \overrightarrow{u}}=\text{ i }k\in R$, to
$k·{\displaystyle \overrightarrow{u}}=$

© 2024 math.edu.pl      kontakt