logowanie

Kąt między wektorami

Kąt między nierównoległymi wektorami ${\displaystyle \overrightarrow{u}}$ i ${\displaystyle \overrightarrow{w}}$ określamy następująco

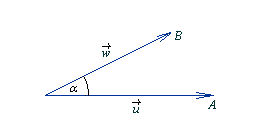
Z dowolnego punktu O kreślimy wektory ${\displaystyle \overrightarrow{OA}}$ i ${\displaystyle \overrightarrow{OB}}$ równe odpowiednio wektorom ${\displaystyle \overrightarrow{u}\text{ i }\overrightarrow{w}}$. W płaszczyźnie wyznaczonej przez wektory ${\displaystyle \overrightarrow{OA}}$ i ${\displaystyle \overrightarrow{OB}}$ otrzymujemy dwa kąty o miarach łukowych odpowiednio α i 2π - α. Ten z otrzymanych kątów, którego miara jest mniejsza od kąta półpełnego nazywamy kątem między wektorami ${\displaystyle \overrightarrow{u}\text{ i }\overrightarrow{w}}$.

Kątem między dwoma niezerowymi wektorami ${\displaystyle \overrightarrow{u}}$ i ${\displaystyle \overrightarrow{w}}$ nazywamy kąt wypukły, którego jedno ramię ma kierunek i zwrot wektora ${\displaystyle \overrightarrow{u}}$, a drugie ramię ma kierunek i zwrot wektora ${\displaystyle \overrightarrow{w}}$.

Kąt między wektorami zgodnie równoległymi jest równy 0, a między wektorami niezgodnie równoległymi jest równy π.

Jeśli jedno ramię kąta wyróżnimy jako początkowe, a drugie jako końcowe, to taki kąt nazywa się kątem skierowanym. Kąt skierowany, którego ramieniem początkowym jest wektor ${\displaystyle \overrightarrow{u}}$, a końcowym ${\displaystyle \overrightarrow{w}}$, oznaczamy $\angle ({\displaystyle \overrightarrow{u}},{\displaystyle \overrightarrow{w}})$.

Miara kąta skierowanego może przyjmować wartości dodatnie lub ujemne. Zależy to od zwrotu kąta skierowanego, czyli od kierunku w którym należy obrócić ramię początkowe, aby otrzymać ramię końcowe. Wartość dodatnią przypisuje się kątom o zwrocie zgodnym z kątem o ramieniu początkowym na dodatniej półosi OX układu współrzędnych i ramieniu końcowym na dodatniej półosi OY. Oznacza to obrót ramienia końcowego przeciwnie do ruchu wskazówek zegara w stosunku do położenia ramienia początkowego.

Kątem między wektorem a osią nazywamy kąt między wektorem a wersorem osi.

Płaszczyzna

Jeżeli ${\displaystyle \overrightarrow{u}}=\text{ i }{\displaystyle \overrightarrow{w}}=$, to
$\cos \alpha =\frac{u_x{w}_x+u_y{w}_y}{{\displaystyle \overrightarrow{\left|u\right|}}·{\displaystyle \overrightarrow{\left|w\right|}}}$

Przestrzeń

Jeżeli ${\displaystyle \overrightarrow{u}}=\text{ i }{\displaystyle \overrightarrow{w}}=$, to
$\cos \alpha =\frac{u_x{w}_x+u_y{w}_y+u_z{w}_z}{{\displaystyle \overrightarrow{\left|u\right|}}·{\displaystyle \overrightarrow{\left|w\right|}}}$

© 2024 math.edu.pl      kontakt