Kwadrat logiczny

Twierdzenia matematyczne na ogół mają postać implikacji. Jeżeli implikacja p ⇒ q jest twierdzeniem, to jego poprzednik p nazywamy założeniem, następnik q - tezą założenia.

Jeżeli implikacja p ⇒ q jest twierdzeniem, to p jest warunkiem wystarczającym na to, aby q, a q warunkiem koniecznym na to, aby p.

Dla danej implikacji p ⇒ q, którą nazywamy prostą, implikację q ⇒ p nazywamy odwrotną. Prawdziwość jednej z nich na ogół nie pociąga za sobą prawdziwości drugiej. Dla każdej implikacji prostej p ⇒ q implikację ~q ⇒ ~p nazywamy przeciwstawną, a implikację ~p ⇒ ~q - przeciwną. Implikacja prosta i przeciwstawna są równoważne oraz implikacje odwrotna i przeciwna są równoważne. Zależności te można przedstawić na kwadracie, który nazywa się kwadratem logicznym.

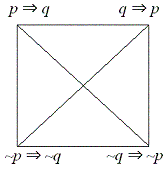
Przy wierzchołkach kwadratu położonych wzdłuż tej samej przekątnej umieszczone są implikacje równoważne. Każda z par implikacji: prosta i przeciwna oraz odwrotna i przeciwstawna stanowi tzw. zamknięty układ implikacji

Dla dowodu twierdzenia postaci p ⇔ q, wystarczy udowodnić implikację prostą p ⇒ q i odwrotną q ⇒ p Z kwadratu logicznego wynika, że dla dowodu twierdzenia p ⇔ q wystarczy udowodnić jedną z par implikacji występujących w tym kwadracie przy wspólnym boku.