Mosty królewieckie
W Królewcu (w Prusach) jest wyspa zwana Kneiphof " - oto początek zdania z pracy Eulera Solutio problematis ad geometriam situs pertinetis, w której formułuje on słynne zadanie o mostach królewieckich:

Czy można po siedmiu mostach łączących dzielnice miasta z wyspą na Pregole odbyć spacer w ten sposób, by przejść kolejno przez wszystkie mosty nie przechodząc po żadnym z nich więcej niż raz jeden.
Odpowiedź Eulera brzmiała: Nie!
Sytuację można przedstawić na grafie:
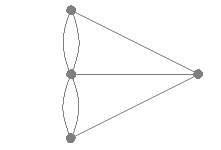
Trzeba w tym grafie znaleźć cykl Eulera, czyli cykl przechodzący przez
wszystkie wierzchołki i wszystkie krawędzie tego grafu, ale przez każdą
krawędź tylko raz.
W opublikowanej w 1736 roku pracy Euler sformułował pierwsze
twierdzenie teorii grafów, które dziś zapisujemy następująco:
W grafie można znaleźć cykl Eulera wtedy i tylko wtedy, gdy graf jest spójny i każdy jego wierzchołek ma parzysty stopień.
Znając to twierdzenie zawsze można stwierdzić, czy łamigłówka typu "narysuj figurę nie odrywając ołówka od kartki" ma rozwiązanie.
Figury, które można nakreślić jednym pociągnięciem ołówka, nie
prowadząc go nigdy po linii już nakreślonej, nazywają się
unikursalne.
Jak rozpoznać figurę unikursalną? Figura jest unikursalna, gdy nie ma
w niej punktów rzędu nieparzystego, lub jeśli są na niej dwa takie
punkty.
Graf mostów królewieckich ma ich trzy; znana dobrze wszystkim
koperta ma dwa takie punkty.