Pochodna funkcji

Niech funkcja f będzie określona w pewnym otoczeniu U punktu x₀. Oznaczmy symbolem Δx przyrost zmiennej niezależnej x, gdzie x∈U(x₀, δ) i x ≠ x₀, symbolem Δy - przyrost wartości funkcji, jaki odpowiada przyrostowi Δx.
Mamy więc Δy = f(x₀ + Δx) - f(x₀).

Ilorazem różnicowym funkcji f w punkcie x₀ dla przyrostu Δx zmiennej x nazywamy stosunek     $\frac{f(x_0+\Delta x)-f\left(x_0\right)}{\Delta x}$

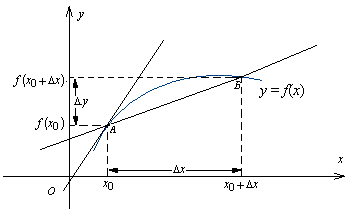
Granicę właściwą ilorazu różnicowego przy Δx→0 nazywamy pochodną funkcji f w punkcie x₀ i oznaczamy symbolicznie f '(x₀)

Mamy więc f '(x₀) = ${\displaystyle \underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f\left(x_0\right)}{\Delta x}=\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}}$

Geometrycznym odpowiednikiem istnienia granicy jest istnienie prostej stycznej w punkcie A = (x₀, f(x₀)) do wykresu funkcji y = f(x)

Funkcję f nazywamy różniczkowalną w przedziale X wtedy, gdy ma pochodną w każdym punkcie tego przedziału.

Różnicą funkcji f w punkcie x₀ dla przyrostu Δx zmiennej niezależnej x nazywamy iloczyn f '(x₀)Δx, przyrost Δx nazywamy różniczką zmiennej niezależnej x.

Granicę właściwą ${\displaystyle \underset{\Delta x\to 0^{-}}{\lim }\frac{f(x_0+\Delta x)-f\left(x_0\right)}{\Delta x}}$ nazywamy pochodną lewostronną funkcji f w punkcie x₀,
Granicę właściwą ${\displaystyle \underset{\Delta x\to 0^{+}}{\lim }\frac{f(x_0+\Delta x)-f\left(x_0\right)}{\Delta x}}$ nazywamy pochodną prawostronną funkcji f w punkcie x₀.

Analogicznie do granic funkcji można też mówić o pochodnych niewłaściwych (nieskończonych) funkcji f w punkcie x₀, jak również o pochodnych niewłaściwych jednostronnych w punkcie x₀.

Jeżeli granica ${\displaystyle \underset{\Delta x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f\left(x_0\right)}{\Delta x}=\infty }$ (-∞), to mówimy, że funkcja f ma w punkcie x₀ pochodną niewłaściwą.
Zapisujemy wówczas f '(x₀) = ∞ lub f '(x₀) = -∞.
Geometrycznie oznacza to, że styczna do wykresu funkcji f w punkcie o odciętej x₀ jest prostopadła do osi OX.

Jeżeli funkcja f ma pochodną f ' w przedziale X i funkcja g(x) = f '(x) ma w punkcie x₀∈X pochodną, to pochodną tę nazywamy pochodną rzędu drugiego funkcji f w punkcie x₀ i symbolicznie oznaczamy f ''(x₀).
Podobnie określa się pochodne rzędu trzeciego, czwartego itd.