Równanie ogólne prostej
W prostokątnym układzie współrzędnych weźmy pod uwagę punkt
P(x1, y1) i wektor niezerowy
.
Ponieważ wektor
jest niezerowy, więc jego współrzędne A i B nie mogą jednocześnie być równe zeru.
Istnieje jedna i tylko jedna prosta l przechodząca przez punkt P i prostopadła do
wektora
określona równaniem
Ax + By + C = 0.
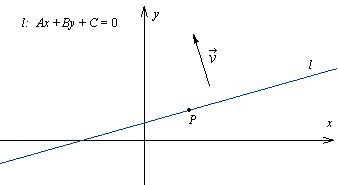
Dla A, B, C ∈ R, przy czym A i B nie są
jednocześnie równe zeru, prosta to zbiór punktów, których współrzędne spełniają zależność:
Ax + By + C = 0
Liczby A, B, C nazywamy współczynnikami liczbowymi równania prostej.
Wektor o współrzędnych jest wektorem kierunkowym prostej. Jest on do tej prostej równoległy. Wektor jest prostopadły do prostej.
Jeśli A = 0, to prosta jest równoległa do osi OX, jeśli B = 0 to prosta jest równoległa do osi OY, jeśli C = 0, to prosta przechodzi przez początek układu współrzędnych.
Gdy B = 0, równanie Ax + By + C = 0 przybiera postać Ax + C = 0,
a ponieważ A ≠ 0, można je napisać w postaci
.
Przedstawia ono prostą równoległą do osi OY i przecinającą oś OX w punkcie
o odciętej
.
Gdy B ≠ 0, równanie Ax + By + C = 0 można napisać w postaci
.
Jest to równanie kierunkowe prostej, gdzie
i
.