Zbiór zadań, (zadania różne)
Zadanie 110
Istnieje tylko jeden trójkąt o takiej własności, że długości jego boków i jednej z wysokości są czterema kolejnymi liczbami naturalnymi. Jakie są długości boków tego trójkąta?
Rozwiązanie
Niech n ≥ 3 będzie liczbą naturalną, zaś liczby n - 2, n - 1, n, n + 1 długościami boków i jednej z wysokości pewnego trójkąta. Oznaczmy także przez a i b długości odcinków, na które wysokość ta dzieli bok tego trójkąta. Rozpatrzmy sytuację, w której h = n - 2 oraz a + b = n. 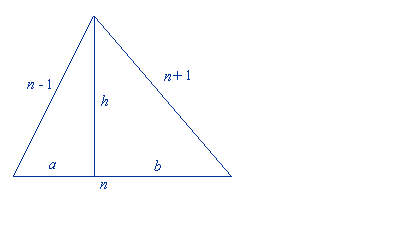
Z równości a2 + h2 = (n - 1)2 i b2 + h2 = (n + 1)2 otrzymujemy związek
(b - a)(b + a) = 4n, skąd b - a = 4, czyli b = a + 4.
W takim razie n = 2a + 4.
Stąd (2a + 2)2 = (n - 2)2 = h2 = (n - 1)2 - a2 = (2a + 3)2 - a2 = 3(a + 3)(a + 1).
Zatem 4(a + 1) = 3(a + 3), skąd a = 5, wówczas b = 9, n = 14. Trójkąt o żądanych własnościach został znaleziony. Przypadki, w których wysokość h jest różne od n - 2 nie spełnia warunków zadania. Trójkąt szukany ma zatem boki długości 13, 14, 15 oraz wysokość o długości 12 opuszczoną na bok o długości 14. Łatwo sprawdzić z tw. Pitagorasa prawdziwość tego trójkąta.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>