Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 118

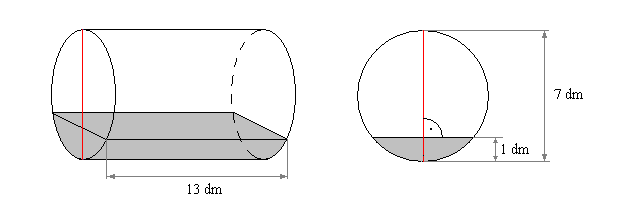
Zbiornik paliwa w kształcie walca usytuowany jest w pozycji poziomej (rysunek) i ma następujące wymiary: długość zbiornika: 13 dm, średnica podstawy: 7 dm. Zbiornik posiada podziałkę objętości (czerwona linia). Ile pełnych litrów paliwa znajduje się w tym zbiorniku, gdy wskaźnik na podziałce jest na wysokości 1 dm?

Rozwiązanie

Objętość całego zbiornika równa jest $V = π \cdot {(3.5)}^{2} \cdot 13 \approx 500$ litrów. Objętość paliwa określonego w zadaniu równa jest iloczynowi pola odcinka koła (część zacieniowana) i długości zbiornika.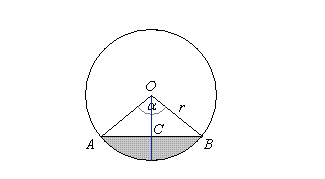

Przyjmijmy π = 3.1416;
Pole odcinka koła o kącie środkowym α równe jest $P = \frac{α}{360 °} π r^{2} - \frac{r^{2} sin α}{2}$
Niewiadomą jest miara kąta α.
Zauważmy, że w naszym przypadku długość odcinka OC = r - 1 dm = 3,5 dm - 1 dm = 2,5 dm. Znając wartość przyprostokątnej i przeciwprostokątnej trójkąta BOC, możemy obliczyć miarę połowy kąta α z funkcji trygonometrycznych: $c o s \frac{α}{2} = \frac{| O C |}{| O B |}$ , stąd $α = \frac{2 \cdot 180 \cdot a r c c o s (\frac{| O C |}{| O B |})}{π} \approx 88.83 °$ . Podstawiając do wzoru na pole odcinka koła otrzymujemy P ≈ 3.37 dm². Objętość naszego paliwa wynosi V ≈ 3.37 dm² · 13 dm ≈ 43.8 dm³.
W zbiorniku znajduje się 43 pełnych litrów paliwa.

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>