Zbiór zadań, (zadania różne)
Zadanie 129
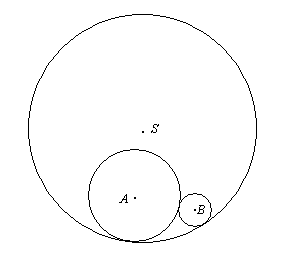
Dany jest okrąg o środku S i promieniu długości 12 oraz dwa okręgi położone tak jak na rysunku. Ile wynosi obwód trójkąta, którego wierzchołkami są środki tych okręgów?
Rozwiązanie
Niech r1 będzie promieniem okręgu o środku A, a r2 - promieniem okręgu o środku B.
Wówczas |SB| = 12 - r2, |SA| = 12 - r1, |AB| = r1 + r2.
Obwód równy jest |AB| + |SB| + |SA| = (r1 + r2) + (12 - r2) + (12 - r1) = 24.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>