Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 131

Pewien chłopiec zabłądził w lesie, który ma kształt trójkąta równobocznego. Nie zna wymiarów lasu, ale posługując się specjalnym przyrządem ustalił, że znajduje się o 6 km od jednego z wierzchołków, o 8 km od drugiego z wierzchołków i o 10 km od trzeciego wierzchołka. Jaka jest powierzchnia tego lasu?

Rozwiązanie

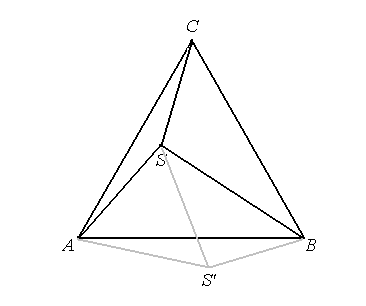
Chłopiec znajduje się w punkcie S. Niech |AS| = 8 km, |BS| = 10 km, |CS| = 6 km. Oznaczmy przez P₁, P₂, P₃ odpowiednio pola trójkątów ABS, BCS, ACS.
Trójkąt ACS obracamy wokół punktu A o 60° w prawo i otrzymujemy trójkąt AS\'B.
Długość odcinka AS\' jest równa długości odcinka AS, kąt SAS\' ma miarę 60°, stąd trójkąt SAS\' jest równoboczny o boku długości 8 km.
W trójkącie SS\'B znamy długości wszystkich boków, wynoszą one 6 km, 8 km, 10 km. Jest to zatem trójkąt prostokątny.
Zauważmy, że P₁ + P₃ = P_ABS + P_ACS = P_AS\'S + P_SS\'B = $\frac{8^{2} \cdot \sqrt{3}}{4} + \frac{8 \cdot 6}{2} = \frac{8^{2} \cdot \sqrt{3}}{4} + 24$ .

Wykonując w analogiczny sposób obroty o 60° trójkąta ABS wokół punktu B i trójkąta BCS wokół punktu C otrzymujemy równania:
$P_{1} + P_{2} = \frac{1 0^{2} \cdot \sqrt{3}}{4} + 24$
$P_{2} + P_{3} = \frac{6^{2} \cdot \sqrt{3}}{4} + 24$
Dodając równania stronami otrzymujemy
$2 P_{1} + 2 P_{2} + 2 P_{3} = \frac{\sqrt{3}}{4} (6^{2} + 8^{2} + 1 0^{2}) + 72$
$2 (P_{1} + P_{2} + P_{3}) = \frac{\sqrt{3}}{4} \cdot 200 + 72$
$P_{A B C} = 25 \sqrt{3} + 36 \approx 79,3$ km²
Powierzchnia lasu ma w przybliżeniu 79,3 km²

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>