Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 165

Trójkąt o polu 450 i kątach wewnętrznych 40°, 60°, 80° podzielić najkrótszym odcinkiem na dwie części o jednakowych polach. Jaka jest długość tego odcinka?

Rozwiązanie

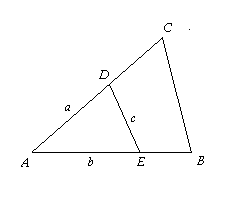
Niech odcinek DE będzie szukanym odcinkiem. Oznaczmy a = |AD|, b = |AE|, c = |DE|.
$c^{2} = a^{2} + b^{2} - 2 a b cos A = (a - b)^{2} + 2 a b (1 - cos A)$
Pole trójkąta ADE wyraża się wzorem $\frac{1}{2} a b sin A$ i jest równe $\frac{1}{2} P$ , gdzie P oznacza pole trójkąta ABC, zatem $a b = \frac{P}{sin A}$ .
Mamy $c^{2} = (a - b)^{2} + 2 P tg \frac{A}{2}$ .
Odcinek c jest najkrótszy, gdy a = b i kąt A jest najmniejszym kątem trójkąta ABC.
W naszym przypadku mamy:
$c^{2} = 2 \cdot 450 \cdot t g 2 0^{\circ}$
$c = 30 \cdot \sqrt{0.364} \approx 18.1$ .
Długość najkrótszego odcinka wynosi w przybliżeniu 18,1.

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>