Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 167

Cztery jednakowe kule o promieniu 1 stykają się każda z każdą. Jaki jest promień najmniejszej kuli, która je wszystkie obejmuje?

Rozwiązanie

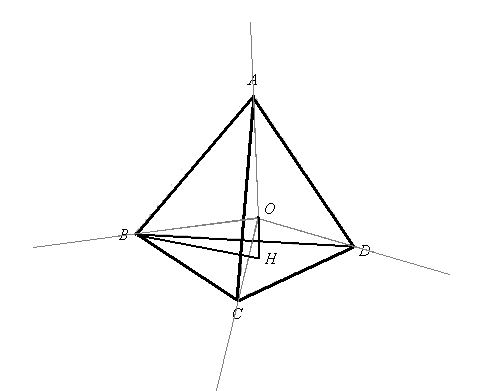
Środki A, B, C, D kul danych są wierzchołkami czworościanu foremnego o krawędzi 2r, gdzie r = 1. Niech O będzie środkiem kuli opisanej na czworościanie ABCD, a R promieniem tej kuli.

Rozpatrzmy szukaną kulę K o środku O i promieniu R + r. Obejmuje ona wszystkie dane kule i jest do nich styczna wewnętrznie w punktach leżących na przedłużeniu odcinków OA, OB, OC, OD w odległości R + r od punktu O.

Środek O kuli K leży na wysokości AH czworościanu ABCD, odcinek BH jest promieniem koła opisanym na trójkącie równobocznym BCD o boku długości 2r.
$| B H | = \frac{2 r}{\sqrt{3}}$
Niech kąt OAB = x. W trójkącie AOB mamy cosx = $\frac{A B}{2 A O} = \frac{r}{R}$
$R = \frac{r}{cos x}$

Z trójkąta ABH $cos x = \frac{A H}{A B} = \sqrt{\frac{2}{3}}$
$R = r \sqrt{\frac{3}{2}} \approx 1.44$

Kula K ma promień równy R + r ≈ 1,44 + 1 ≈ 2,22.

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>