Zbiór zadań, (zadania różne)
Zadanie 168
Ile wynosi promień najmniejszego koła, w którym zmieści się dowolny trójkąt o bokach nie dłuższych niż 1?
Rozwiązanie
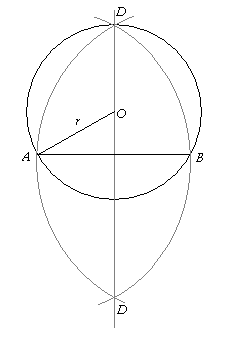
Niech AB będzie bokiem trójkąta ABC, który nie jest krótszy od żadnego z pozostałych boków.
Zakładamy, że długość boku AB jest mniejsza lub równa 1.
Zakreślamy z punktów A i B jako ze środków okręgi o promieniu równym odcinkowi AB.
Trójkąt ABC znajduje się w jednym z obszarów ograniczonych przez odcinek AB i przez dwa łuki tych okręgów.
Trójkąt ABC zatem leży w kole opisanym na trójkącie ABD. Promień r koła opisanego równy jest .
Ponieważ AB jest mniejsze lub równe 1, zatem każdy trójkąt o bokach nie dłuższych niż 1 mieści się w kole o promieniu .
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>