Zbiór zadań, (zadania różne)
Zadanie 170
Przez środek ciężkości trójkąta poprowadzono prostą, dzieląc ten trójkąt na dwie części. Jaką częścią pola całego trójkąta jest pole najmniejszej z tych części?
Rozwiązanie
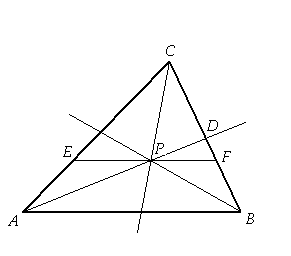
Niech P będzie środkiem ciężkości trójkąta ABC o polu równym S.
Gdy trójkąt rozetniemy wzdłuż jednaj ze środkowych. np. wzdłuż AD podzielimy go na dwa trójkąty o równych polach.
Dzieląc trójkąt ABC wzdłuż odcinka przechodzącego przez punkt P i równoległego do boku AB, podzielimy ten trójkąt na trójkąt EFC i trapez ABFE. Trójkąt EFC jest podobny do trójkąta ABC w skali . Stosunek pól figur podobnych równy jest kwadratowi skali podobieństwa. Więc pole trójkąta EFC równe jest , pole trapezu równe jest .
Trójkąt EFC jest najmniejszą częścią, o której mowa w zadaniu i jest równy pola całego trójkąta.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>