Zbiór zadań, (zadania różne)
Zadanie 180
W kole o promieniu 30 zaznaczono punkt A odległy od środka koła o 18. Ile różnych cięciw o długości wyrażającej się liczbą całkowitą przechodzi przez punkt A?
Rozwiązanie
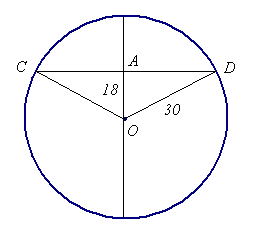
Najkrótsza cięciwa przechodząca przez punkt A to cięciwa CD, prostopadła do odcinka OA, gdzie O jest środkiem koła.
Z twierdzenia Pitagorasa wynika, że |CD| =
Najdłuższą cięciwą przechodząca przez punkt A jest średnica o długości 60.
Pozostałe cięciwy będą miały długości od 49 do 59, przy czym każda z nich jest długością dwóch cięciw przechodzących przez punkt A, symetrycznych względem prostej AO
Razem 1 + 1 + 2 · 11 = 24
Przez punkt A przechodzą 24 cięciwy o długości wyrażającej się liczbą całkowitą.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>