Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 193

Punkt S znajdujący się wewnątrz kwadratu ABCD jest odległy od wierzchołków A, B, C odpowiednio o 2, 7 i 9. Jaka jest odległość punktu S od wierzchołka D?

Rozwiązanie

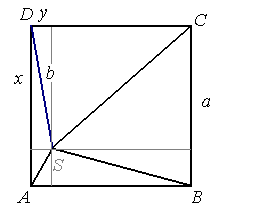
Niech a oznacza długość boku kwadratu, b - szukana odległość punktu S od wierzchołka D.
Wówczas na mocy tw. Pitagorasa:
$x^{2} + y^{2} = b^{2}$
$(a - x)^{2} + y^{2} = 4$
$x^{2} + (a - y)^{2} = 81$
$(a - x)^{2} + (a - y)^{2} = 49$

Dodając stronami rówanie drugie i trzecie otrzymujemy:
$x^{2} + y^{2} + (a - x)^{2} + (a - y)^{2} = 85$
i podstawiając do niego równanie czwarte otrzymujemy
$x^{2} + y^{2} = 36$
Stąd na mocy równania pierwszego mamy $b^{2} = 36$
b = 6

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>