Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 196

Jaka jest najmniejsza powierzchnia kartki papieru w kształcie kwadratu, którą można owinąć sześcian o krawędzi długości 3?

Rozwiązanie

Rozpatrując dowolną siatkę sześcianu, wydaje się, że musi to być arkusz w kształcie kwadratu o boku długości cztery razy dłuższej od długości krawędzi sześcianu. Jednak jest rozwiązanie, za pomocą którego do owinięcia sześcianu wystarczy arkusz papieru o powierzchni dwukrotnie mniejszej.

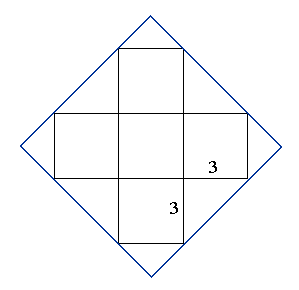
Rysunek powyżej przedstawia siatkę sześcianu bez jednej ściany wpisaną w kwadrat. Takim arkuszem kwadratowym można owinąć sześcian, trójkąty przy wierzchołkach pokryją szóstą ścianę sześcianu. Trójkąty na brzegach to fragmenty kartki, które zostaną zagięte i nałożą się na inną warstwę papieru.

Długość boku kwadratu wynosi $2 \cdot \sqrt{3^{2} + 3^{2}} = 6 \sqrt{2}$
Pole powierzchni kwadratu równe jest $(6 \sqrt{2})^{2} = 72$ i to jest najmniejsza powierzchnia kartki papieru w kształcie kwadratu jaką można owinąć sześcian.

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>