Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 200

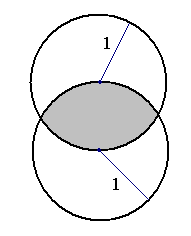
Dwa jednakowe okręgi, każdy o promieniu długości 1, przecinają się tak, że odległość ich środków jest równa długości promienia. Oblicz pole zacieniowanej figury.

Rozwiązanie

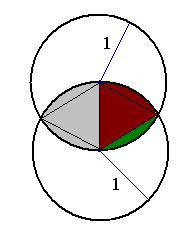
Obszar zaznaczony na czerwono to wycinek koła o kącie środkowym 60 stopni.
Pole wycinka koła o promieniu r równe jest $\frac{π r^{2}}{6}$ .
Pole trójkąta równobocznego o boku długości r równe jest $\frac{\sqrt{3} r^{2}}{4}$
Pole obszaru zaznaczonego na zielono równe jest: $\frac{π r^{2}}{6} - \frac{\sqrt{3} r^{2}}{4} = \frac{2 π - 3 \sqrt{3}}{12} r^{2}$

Pole rozważanej figury jest sumą pól dwóch trójkątów równobocznych o bokach długości 1 i czterech obszarów zaznaczonych na zielono.
$P = 4 \cdot \frac{2 π - 3 \sqrt{3}}{12} r^{2} + 2 \cdot \frac{r^{2} \sqrt{3}}{4} = \frac{4 π - 3 \sqrt{3}}{6} r^{2}$ .

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>