Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 209

Jakie jest największe pole trójkąta, którego długość boku najkrótszego wynosi 1, a najdłuższego wynosi 3?

Rozwiązanie

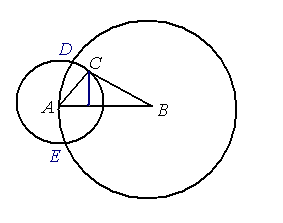
Wykreślmy dwa okręgi, jeden o środku w punkcie A i promieniu 1, drugi o środku w punkcie B i promieniu 3. Trzeci wierzchołek trójkąta będzie leżał na łuku DE.
Pole trójkąta równe jest $\frac{| A B | \cdot h}{2} = \frac{3}{2} h$ .
Aby pole było największe, największa musi być wysokość h, czyli wierzchołek C musi pokrywać się z jednym z punktów E lub D. Trójkąt ABC ma największa pole, jeśli jest równoramienny o bokach długości 1, 3, 3.
Pole trójkąta równoramiennego o bokach 1, 3, 3 równe jest $\frac{\sqrt{35}}{4} \approx 1.479$ .

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>