Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 212

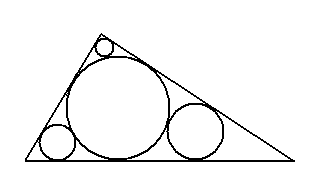
W trójkąt wpisano okrąg oraz trzy mniejsze okręgi w taki sposób, że każdy z pozostałych okręgów jest styczny do okręgu największego i do dwóch boków trójkąta. Długości promieni czterech okręgów są czterema różnymi liczbami całkowitymi. Jaki jest możliwie najmniejszy promień okręgu największego?

Rozwiązanie

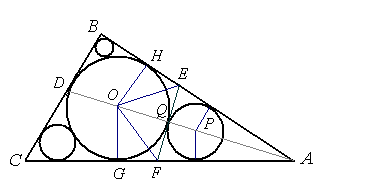
Niech r₁ będzie promieniem okręgu największego, r₂, r₃, r₄ promieniami pozostałych okręgów. Niech promienie OH i OG będą prostopadłe do boków trójkąta, a odcinek EF będzie odcinkiem wspólnej stycznej do obu okęgów.
Cztery kąty przy wierzchołku O są tej samej miary, oznaczmy je przez α, (α = ∠ GOF).
Zachodzi $α = \frac{π - | ∠ B A C |}{4}$
Analogicznie przyjmując oznaczenia w pozostałych okręgach mamy
$β = \frac{π - | ∠ A B C |}{4}$
$γ = \frac{π - | ∠ A C B |}{4}$
Z tych równości wynika $α + β + γ = \frac{π}{2}$
$t g α t g β + t g β t g γ + t g α t g γ = 1$

Trójkąt OFP jest prostokątny, zachodzi $F Q = r_{1} \cdot t g α$ , stąd $t g α = \sqrt{\frac{r_{2}}{r_{1}}}$
Analogicznie $t g β = \sqrt{\frac{r_{3}}{r_{1}}}$ oraz $t g γ = \sqrt{\frac{r_{4}}{r_{1}}}$
Podstawiając te równości do uzyskanego związku dla tangensów otrzymujemy $r_{1} = \sqrt{r_{2} \cdot r_{3}} + \sqrt{r_{2} \cdot r_{4}} + \sqrt{r_{3} \cdot r_{4}}$
Ponieważ promienie mają być liczbami całkowitymi więc iloczyny odpowiednich promieni muszą być kwadratami liczb naturalnych.
Najmniejszą wartość promienia najwięszkego okręgu otrzymujemy dla $r_{2} \cdot r_{3} = 4$ , $r_{2} \cdot r_{4} = 9$ , $r_{3} \cdot r_{4} = 36$
Wóczas $r_{1} = \sqrt{4} + \sqrt{9} + \sqrt{36} = 11$ .

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>