Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 218

Pięć kul o różnej wielkości znajduje się w stożkowym lejku, gdzie każda z kul jest styczna do sąsiadującej kuli oraz do lejka. Najmniejsza z kul ma promień 8, największa 18. Jaki promień ma kula środkowa?

Rozwiązanie

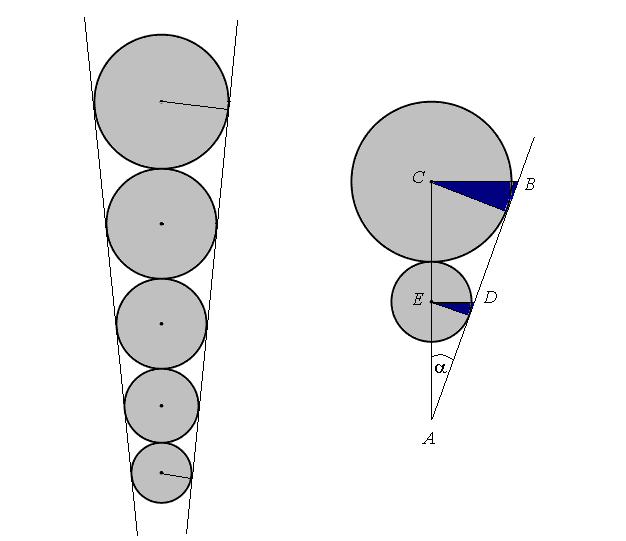
Rysunek z lewej strony przedstawia przekrój osiowy stożkowego lejka, gdzie promienie kół odpowiadają promieniom odpowiednich kul.
Rozważmy dowolne dwa sąsiednie kule o promieniach r₁ i r₂ na rysunku po prawej stronie.
Ponieważ każde dwie kule są ze sobą styczne, więc odległość ich środków równa jest r₁ + r₂. Kule styczne są także z powierzchnią boczną stożkowego lejka, gdzie nachylenie jest stałe, stąd trójkąty zaznaczone kolorem niebieskim są podobne.
Trójkąt ABC jest prostokątny, więc odległość pozioma od środka kuli do powierzchni bocznej równa jest odpowiednio |BC| = r₁ · s i |DE| = r₂ · s, gdzie s jest stałą zależną od kąta α, $s = \frac{A B}{A C} = \frac{A D}{A E}$ .
Niech $k = \frac{r_{1}}{r_{2}}$ , z tw. Talesa wnioskujemy, ze stosunek promieni sąsiednich kul jest stały (zależy od kąta α).
Długości promieni kul tworzą ciąg geometryczny. Środkowy wyraz ciągu geometrycznego jest średnią geometryczną wyrazu pierwszego i ostatniego.
$r_{s r} = \sqrt{8 \cdot 18} = 12$

Ogólnie dla nieparzystej liczby kul, długość promienia środkowej kuli jest średnią geometryczną długości promieni kul najmniejszej i największej.

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>