Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 221

W trójkąt o bokach długości 10, 17, 21, wpisano kwadrat, którego dwa wierzchołki leżą na najdłuższym boku trójkąta, a pozostałe dwa leżą na pozostałych bokach trójkąta. Oblicz pole wpisanego kwadratu.

Rozwiązanie

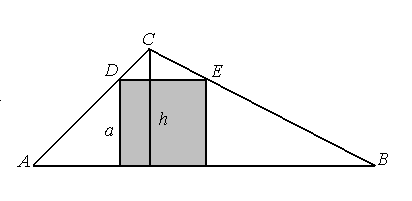
Korzystając ze wzoru Herona na pole trójkąta $P = \sqrt{p (p - a) (p - b) (p - c)}$ , gdzie p jest połową obwodu $p = \frac{1}{2} (a + b + c)$ , pole trójkąta o bokach 10, 17, 21 równe jest $\sqrt{24 \cdot (24 - 10) \cdot (24 - 17) \cdot (24 - 21)} = 84$ .
Ze wzoru na pole trójkąta mamy $84 = \frac{21 \cdot h}{2}$ , skąd h = 8.
Trójkąt DEC jest podobny do trójkąta ABC, więc stosunek wysokości do podstawy w obu trójkątach jest jednakowy.
$\frac{8}{21} = \frac{8 - a}{a}$
Po przekształceniach otrzymujemy długość boku kwadratu $a = \frac{168}{29}$
Pole kwadratu równe jest $(\frac{168}{29})^{2} \approx 33.56$ .

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>