Zbiór zadań, (zadania różne)
Zadanie 222
Jakie jest największe pole powierzchni półkola wpisanego w kwadrat o polu 1?
Rozwiązanie
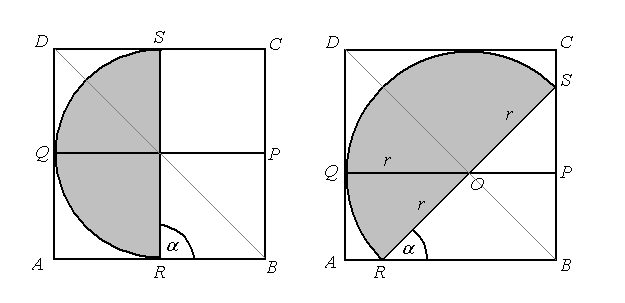
Półkole wpisane w kwadrat na rysunku po lewej stronie jest styczne z brzegiem kwadratu w trzech punktach.
Średnica tego półkola równa jest 1, a powierzchnia wynosi .
Rozważmy półkole na rysunku po prawej stronie. Końce średnicy półkola R i S leżą na dwóch sąsiednich bokach kwadratu, a półokrąg jest styczny do pozostałych boków. Tak wpisane półkole ma cztery punkty wspólne z brzegiem kwadratu i intuicyjnie wydaje się być największym.
Przez środek średnicy półkola prowadzimy odcinek PQ równoległy do boku AB. Punkt Q jest punktem styczności, a odcinek OQ jest promieniem półkola.
Trójkąty RBS i OPS są podobne, stąd
Długość odcinka PQ równa jest 1, więc r + |OP| = 1
r + r cosα = 1
Półkole jest symetryczne względem przekątnej BD, więc kąt α = 45°.
Dla α = 45° mamy . Stąd .
Dla tak wpisanego półkola, jego powierzchnia równa jest .
Czy dla kąta α = 45° półkole ma największą powierzchnię?
Dla α = 90° (rysunek po lewej) powierzchnia półkola jest mniejsza.
Obracając półkole zgodnie z ruchem wskazówek zegara i przesuwając je po przekątnej BD tak, aby półokrąg był styczny do dwóch sąsiednich boków kwadratu oraz koniec R średnicy leżał na boku AB, zmniejszamy kąt α jednocześnie zwiększając powierzchnię półkola. Podczas takiego "obracania" półkola, drugi koniec średnicy S będzie znajdował się wewnątrz kwadratu.
Dla kąta α < 45° promień r wzrasta, ale koniec S średnicy półkola będzie znajdował się już poza kwadratem. Stąd największa powierzchnia półkola jest dla α = 45°.
Dla tej wartości, jeśli do półokręgu dorysujemy drugi półokrąg dopełniając go do okręgu, to okrąg ten będzie przechodził przez wierzchołek B.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>