Zbiór zadań. Rozwiązanie zadania

Zbiór zadań, (zadania różne)

Zadanie 240

Jaka jest najmniejsza liczba nieprzystających kwadratów o bokach całkowitych, z których można zbudować prostokąt?

Rozwiązanie

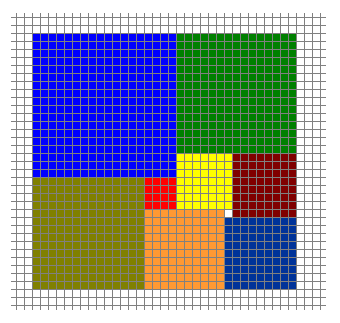
Za pomocą dziewięciu nieprzystających kwadratów można zbudować prostokąt.

(69 × 61): 36, 33, 28, 25, 16, 9, 7, 5, 2
(33 × 32): 18, 15, 14, 10, 9, 8, 7, 4, 1

Graf skierowany zbudowany w określony sposób odpowiada zbiorowi n-kwadratów, z którego może być utworzony pewien prostokąt.

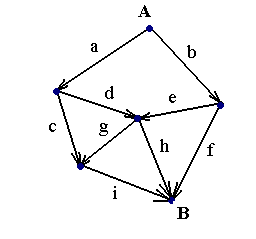
Wierzchołki umieszczamy na różnych poziomach. Każdej krawędzi nadajemy kierunek od wierzchołka leżącego wyżej do wierzchołka leżącego niżej. Poruszając się z wierzchołka górnego A do wierzchołka dolnego B dowolną ścieżką, suma wag musi być zawsze jednakowa, oraz suma wag krawędzi wychodzących z wierzchołka jest równa sumie wag krawędzi wchodzących do tego wierzchołka.

Można zapisać to algebraicznie:
a - c - d = 0
b - e - f = 0
c + g - i = 0
d + g - c = 0
f - h - e = 0
h - i - g = 0
d + e - g - h = 0
b + e - d - a = 0
Są to wszystkie niezależne zależności dla powyższego grafu. Mamy układ 8 równań z dziewięcioma niewiadomymi. Po przekształceniach otrzymujemy zależności:
$b = \frac{18}{15} a$ ,
$c = \frac{8}{15} a$ ,
$d = \frac{7}{15} a$ ,
$e = \frac{4}{15} a$ ,
$f = \frac{14}{15} a$ ,
$g = \frac{1}{15} a$ ,
$h = \frac{10}{15} a$ ,
$i = \frac{9}{15} a$ ,

Jeśli za a podstawimy 15 to otrzymujemy rozwiązanie w liczbach całkowitych: 15, 18, 8, 7, 4, 14, 1, 10, 9.
Kolejność rozwiązania jest podpowiedzią w jakiej kolejności należy układać kwadraty w rzędach, aby otrzymać prostokąt.

Można ułożyć jeszcze tylko jeden graf (o różnych wagach), gdzie z punktu A wychodzą 3 krawędzie i postępując analogicznie jak wyżej otrzymujemy drugie rozwiązanie: 36, 33, 28, 25, 16, 9, 7, 5, 2

Dla grafu złożonego z 8 lub mniej wierzchołków nie istnieje, żadna taka konfiguracja, w której otrzymamy jako wynik nie powtarzające się liczby całkowite.

Powiązanie z Prawem Kirchhoffa: Jeśli graf ten zamienimy na sieć elektryczną składającą się z przewodników (krawędzie), w której można wyodrębnić kilka obwodów zamkniętych z natężeniem prądu równym wagom tegoż grafu, to natężenie tak się rozgałęzia, że suma natężeń prądów wypływających równa się sumie natężeń prądów wpływających. Suma algebraiczna natężeń prądów zbiegających się w węźle (wierzchołku) równa się zeru.

powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>