Zbiór zadań, (zadania różne)
Zadanie 242
Na nieograniczonej szachownicy stoi skoczek szachowy. Znajdź liczbę pól, na których skoczek może znaleźć się po 4 ruchach.
Rozwiązanie
Po wykonaniu parzystej ilości ruchów, skoczek może znaleĄć się na polu tego samego koloru, co pole zajmowane przez niego na początku.
Jeśli obrócimy szachownicę o 45 stopni i rozważymy pola tego samego koloru, oznaczając tylko środki tych pól. Pola, na które może dostać się skoczek po 2 ruchach można przedstawić za pomocą rysunku.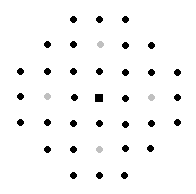
Ilość tych pól jest równa 33 oznaczona kolorem czarnym.
Łącząc te figury otrzymamy figurę złożoną z kwadratu zawierającego 92 = 81 punktów oraz cztery trapezy, z których każdy zawiera 12 punktów. Razem otrzymujemy 129 punktów.
Po 4 ruchach skoczek może dostać się na jedno spośród 129 pól.
Ogólnie, po wykonaniu 2n ruchów otrzymamy figurę rozpadającą się na kwadrat o boku 4n, który zawiera (4n + 1)2 punktów oraz na 4 trapezy, z których każdy zawiera (4n - 1)(4n - 3) + ... + (2n + 1) = 3n2 punktów.
Ogółem otrzymujemy 12n2 + (4n + 1)2 = 28n2 + 8n + 1 punktów.
Po 2n ruchach (dla n > 1) skoczek szachowy może dostać się na jedno spośród 28n2 + 8n + 1 pól.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>