Zbiór zadań, (zadania różne)
Zadanie 250
W kwadracie o boku długości 1 zatoczono z każdego wierzchołka okrąg o promieniu 1. Oblicz obwód części wspólnej otrzymanych w ten sposób kół.
Rozwiązanie
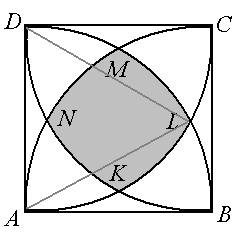Punkty K, L, M, N oznaczają punkty przecięcia się okręgów wewnątrz kwadratu ABCD, a obszar zacieniowany jest częścią wspólną otrzymanych czterech kół. Trójkąt ALD jest równoboczny o boku długości 1, więc łuk LD okręgu o środku w punkcie A stanowi $\frac{1}{6}$ całego okręgu.
Łuk BD stanowi $\frac{1}{4}$ okręgu, zatem długość łuku BL wynosi $\frac{1}{4} \cdot 2\pi - \frac{1}{6} \cdot 2\pi = \frac{1}{6}\pi$.
Analogicznie $|MD| = \frac{1}{6}\pi$.
Stąd $|ML| = \frac{1}{4} \cdot 2\pi - \frac{2}{6}\pi = \frac{1}{6}\pi$.
Obwód zacieniowanej części równy jest $4 \cdot \frac{1}{6}\pi = \frac{2}{3}\pi$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>