Zbiór zadań, (zadania różne)
Zadanie 254
Na trójkącie prostokątnym ABC opisano okrąg. Odległości od punktów A i B do prostej stycznej poprowadzonej przez wierzchołek C kąta prostego wynoszą 9 i 16. Oblicz pole trójkąta prostokątnego ABC.
Rozwiązanie
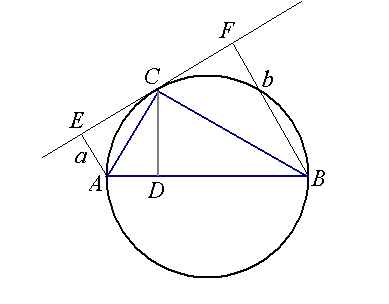
Niech odcinek $CD$ będzie wysokością trójkąta. Z podobieństwa trójkątów $ABC$ i $ADC$ i z tw. o kącie między styczną i sieczną wnioskujemy, że kąty $ACE$ i $ABC$ mają jednakowe miary. Oznacza to, że trójkąt $AEC$ i $ADC$ są przystające oraz $|AD| = a$. Analogicznie $|BD| = b$
Z podobieństwa trójkątów $ADC$ i $ACB$ otrzymujemy $|AC|^2 = |AD| \cdot |AB|$, z podobieństwa trójkątów $BDC$ i $BCA$ wynika $|BC|^2 = |DB| \cdot |AB|$
Zatem $|AC|^2 = a(a+b)$, a $|BC|^2 = b(b+a)$
W zadaniu $a = 9, b=16$, stad przyprostokątne trójkąta mają odpowiednio długości $15$ i $20$, a pole jego wynosi $150$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>