Zbiór zadań, (zadania różne)
Zadanie 264
Wewnątrz trójkąta równobocznego $ABC$ wybrano dowolny punkt $P$. Punkty $D, E, F$ są rzutami prostokątnymi punktu $P$ na boki odpowiednio $AB, BC, CA$. Oblicz wartośc wyrażenia $\frac{|PD| + |PE| + |PF|}{|AD| + |BE| + |CF|}$.
Rozwiązanie
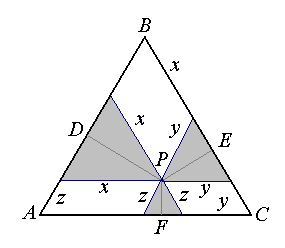
Niech $a$ będzie długością boku trójkąta $ABC$. $PD + PE +PF = \frac{a\sqrt{3}}{2}$.
Prowadząc trzy proste równoległe do boków trójkąta i przechodzące przez punkt $P$ otrzymamy trzy trójkąty równoboczne (zacieniowane). Suma długości ich boków równa jest długości boku trójkąta $ABC$. Mamy $x +y+z = a$. Odcinki $PD, PE, PF$ są wysokościami tych trójkątów, więc $AD + BE + CF = z + \frac{x}{2} + x + \frac{y}{2} + y + \frac{z}{2} = \frac{3}{2}(x+y+z) = \frac{3}{2}a$
Stąd otrzymujemy $\frac{|PD| + |PE| + |PF|}{|AD| + |BE| + |CF|} = \frac{\frac{a\sqrt{3}}{2}}{\frac{3}{2}a} = \frac{\sqrt{3}}{3}$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>