Zbiór zadań, (zadania różne)
Zadanie 266
Kwadrat podzielono na trójkąty tak, aby powstała siatka ostrosłupa. Oblicz pole powierzchni tego ostrosłupa wiedząc, że jego objętość wynosi 72.
Rozwiązanie
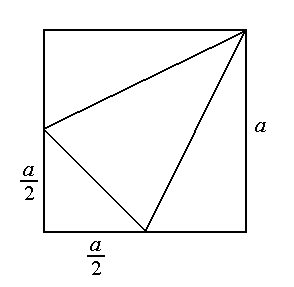
Po złożeniu otrzymamy ostrosłup o podstawie trójkąta prostokątnego równoramiennego o polu $\frac{a^2}{8}$. Wysokość ostrosłupa wynosi $a$, więc objętość jest równa $\frac{a^3}{24}$.
Otrzymujemy, że $\frac{a^3}{24} = 72$, skąd $a = 12$.
Pole powierzchni ostrosłupa równe jest polu kwadratu i wynosi 144.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>