Zbiór zadań, (zadania różne)
Zadanie 271
Każdy bok kwadratu $ABCD$ o polu równym 1 podzielono na trzy równe części. Przez osiem punktów podziału poprowadzono cztery odcinki tak, że powstał kwadrat $KLMN$ obrócony o 45 stopni względem kwadratu $ABCD$. Ile wynosi pole kwadratu $KLMN$?
Rozwiązanie
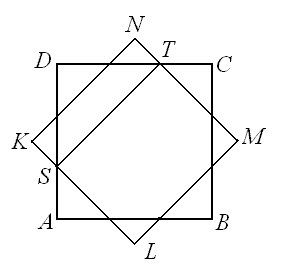
Niech $|AB| = a$, $|ST| = b$, $P_1$ - pole kwadratu $KLMN$, $P$ - pole kwadratu $ABCD$.
Z twierdzenia Talesa mamy $b = \frac{2}{3} \cdot |AC| = \frac{2}{3}a\sqrt{2}$.
Odcinki $ST$ i $KN$ są równoległe.
$\frac{P_1}{P} = \frac{b^2}{a^2} = \frac{(\frac{2}{3}a\sqrt{2})^2}{a^2} = \frac{8}{9}$.
Stąd pole kwadratu $KLMN$ równe jest $\frac{8}{9}$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>