Zbiór zadań, (zadania różne)
Zadanie 272
Ile istnieje różnych sposobów pomalowania wszystkich wierzchołków sześcianu za pomocą dwóch różnych kolorów?
Rozwiązanie
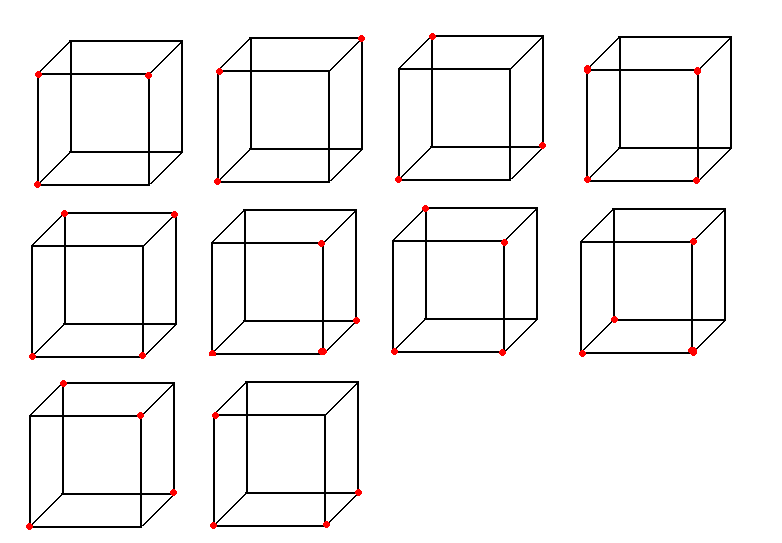
Przyjmijmy, że malujemy wierzchołki sześcianu kolorem czerwonym i białym.
Istnieje:
1 sposób pomalowania wszystkich wierzchołków na kolor biały (bez czerwonych wierzchołków),
1 sposób z jednym czerwonym wierzchołkiem,
3 sposoby z dwoma czerwonymi wierzchołkami (wierzchołki czerwone leżą na jednej krawędzi, na jednej przekątnej ściany lub na jednej przekątnej sześcianu)
3 sposoby z trzema czerwonymi wierzchołkami (trzy wierzchołki leżą na jednej ścianie albo dwie na jednej krawędzi, a trzecia na jednej przekątnej ściany zawierającej jakikolwiek z tych dwóch wierzchołków, albo trzy wierzchołki leżą parami na jednej przekątnej ściany),
7 sposobów z czterema wierzchołkami czerwonymi (wszystkie cztery wierzchołki leżą na jednej ścianie, albo trzy wierzchołki A, B, C leżą na jednej ścianie, a czwarty na krawędzi zawierającej wierzchołek A lub wierzchołek B lub położony diametralnie przeciwnie w stosunku do B, albo dwa wierzchołki na jednej krawędzi, a dwa drugie na krawędzi położonej diametralnie przeciwnie w stosunku do pierwszej krawędzi).
Przypadki, gdy mamy $5, 6, 7, 8$ czerwonych wierzchołków, sprowadzają się do przypadków już rozpatrywanych na drodze zamiany kolorów na odwrotne. Razem otrzymujemy $1+1+3+3+7+3+3+1+1=23$ sposoby pomalowania.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>