Zbiór zadań, (zadania różne)
Zadanie 273
W kole poprowadzono dwie prostopadłe cięciwy. W wyniku przecięcia cięciw otrzymano cztery odcinki o długościach $1, 2, 3, x$. Jaką najmniejszą długość może mieć odcinek $x$?
Rozwiązanie
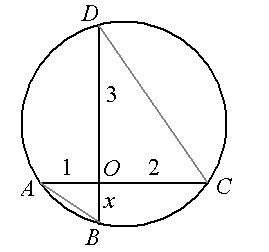
Niech punkty $A$ i $C$ oraz $B$ i $D$ są końcami cięciw, a punkt $O$ ich punktem wspólnym. Rysunek przedstawia sytuację, w której długość odcinka $x$ jest najkrótsza. Trójkąty $AOB$ i $COD$ są podobne.
Otrzymujemy proporcję $\frac{3}{1} = \frac{2}{x}$ skąd $x = \frac{2}{3}$
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>