Zbiór zadań, (zadania różne)
Zadanie 274
Ile wynosi suma miar siedmiu zaznaczonych kątów?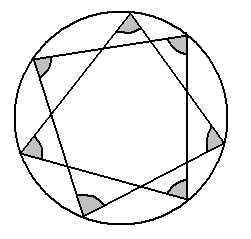
Rozwiązanie
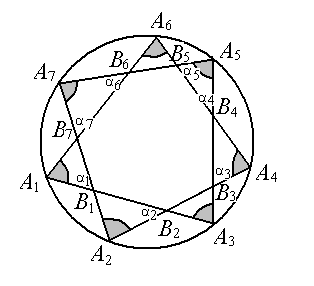
Niech $A_1, A_2, ..., A_7$ oznaczają wierzchołki szukanych kątów, a $B_1, B_2, ..., B_7$ wierzchołki siedmiokąta powstałego w wyniku przecięć cięciw. Suma kątów siedmiokąta $B_1, B_2, ..., B_7$ wynosi $900^\circ$
Zachodzi także $900^\circ = 180^\circ - \alpha_1 + 180^\circ - \alpha_2 + ... + 180^\circ - \alpha_7$
Otrzymujemy zatem $\alpha_1 + \alpha_2 + ... + \alpha_7 = 1260^\circ - 900^\circ = 360^\circ$
Suma miar wszystkich kątów w trójkątach $A_1B_1B_7, A_2B_2B_1, ..., A_7B_7B_6$ wynosi $1260^\circ$.
Suma miar kątów przy wierzchołkach $A_1, A_2, ..., A_7$ równa jest $1260^\circ - 2(\alpha_1 + \alpha_2 + ... + \alpha_7) = 1260^\circ - 720^\circ = 540^\circ$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>