Zbiór zadań, (zadania różne)
Zadanie 276
W sześcian o krawędzi 1 wpisano kulę $K_1$. Ile wynosi promień kuli $K_2$ stycznej zewnętrznie do kuli $K_1$ i do trzech ścian sześcianu?
Rozwiązanie
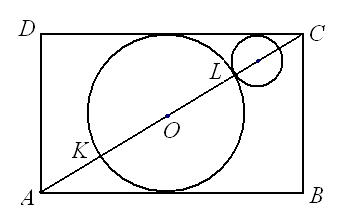
Oznaczmy przez $R$ promień kuli $K_1$, a przez $r$ promień kuli $K_2$.
Rysunek przedstawia przekrój sześcianu płaszczyzną przechodzącą przez przekątne podstaw. Prostokąt $ABCD$ ma boki długości $1$ i $\sqrt2$. Długość przekątnej $AC$ sześcianu wynosi $\sqrt3$, a promień $R$ kuli $K_1$ równy jest $\frac{1}{2}$
Zatem $CL = \frac{\sqrt3}{2}-\frac{1}{2} = \frac{\sqrt3 - 1}{2}$, $CK = \frac{\sqrt3}{2}+\frac{1}{2} = \frac{\sqrt3 + 1}{2}$
Stosując jednokładność $J^k$, gdzie $k = \frac{CL}{CK} = \frac{(\sqrt3 - 1)^2}{2} = 2-\sqrt3$ otrzymujemy $r = Rk = \frac{2-\sqrt3}{2}$
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>