Zbiór zadań, (zadania różne)
Zadanie 281
Środki dwóch sfer o promieniach 29 i 25 są odległe o 36. Ile wynosi długość linii ich przecięcia?
Rozwiązanie
Linia przecięcia to okrąg. Rozpatrzmy przekrój płaszczyzną przechodząca przez środki sfer. 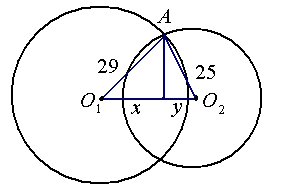
Promień szukanego okręgu, to wysokość $r$ trójkąta $O_1O_2A$ opuszczona na bok $O_1O_2$. Wysokość ta dzieli podstawę na odcinki $x$ i $y$.
Mamy $x+y=36$, zachodzi więc równość:
$29^2-x^2=25^2-y^2$
$x^2-y^2=29^2-25^2$
$(x-y)(x+y) = 216$
Ponieważ $x+y=36$, to $(x-y)\cdot36 = 216$, więc $x-y=6$. Ostatecznie $x=21$, $y=15$
Promień $r$ wyznaczamy z tw. Pitagorasa.
$r^2 = 29^2 - 21^2 $
$r=20$
Obwód szukanego okręgu wynosi $40\pi$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>