Zbiór zadań, (zadania różne)
Zadanie 284
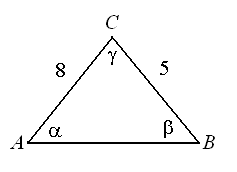
Dwa boki trójkąta o polu równym 16 mają długości 5 i 8. Ile wynosi długość trzeciego boku tego trójkąta?
Rozwiązanie
$P= \frac{1}{2}ab \sin\gamma$
Niech $a=8$, $b=5$. Mamy $16 = \frac{1}{2}\cdot 8 \cdot 5 \cdot \sin\gamma$, skąd $\sin\gamma = \frac{4}{5}$.
Dalej mamy $\cos\gamma = \sqrt{1 - \sin^2\gamma} = \frac{3}{5}$, dla trójkąta ostrokątnego oraz $\cos\gamma = -\frac{3}{5}$ dla trójkąta rozwartokątnego
Korzystając z tw. kosinusów obliczamy długość trzeciego boku dla obu trójkątów:
$AB = \sqrt{8^2 + 5^2 - 48} = \sqrt{41}$
$AB = \sqrt{8^2 + 5^2 + 48} = \sqrt{137}$
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>