Zbiór zadań, (zadania różne)
Zadanie 285
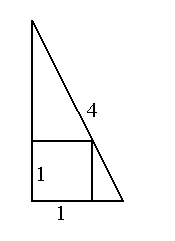
W trójkąt prostokątny o przeciwprostokątnej 4 wpisano kwadrat o boku 1 tak jak na rysunku. Jaką długość ma dłuższa przyprostokątna?
Rozwiązanie
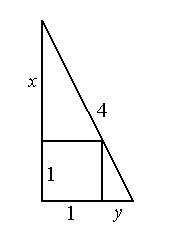
Z trójkątów podobnych mamy $\frac{x}{1} = \frac{1}{y}$, zatem $xy=1$
Z tw. Pitagorasa mamy $(x+1)^2 + (y+1)^2 = 4^2$,
więc $(x+y)^2 +2(x+y)=16$, a $x+y = -1 \pm \sqrt{17}$
Ponieważ $x+y$ musi być dodatnie, więc $x+y = \sqrt{17}-1$ oraz $x-y-\sqrt{(x+y)^2 - 4xy} = \sqrt{14 - 2\sqrt{17}}$
$x = \frac{1}{2} (\sqrt{14 - 2\sqrt{17}} + \sqrt{17}-1)$
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>