Zbiór zadań, (zadania różne)
Zadanie 292
W kwadracie o boku długości $1$ z każdego wierzchołka zatoczono okrąg o promieniu $1$. Oblicz pole części wspólnej otrzymanych w ten sposób kół.
Rozwiązanie
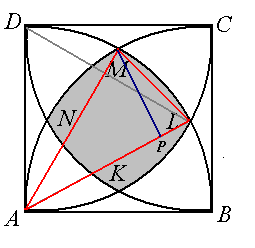
Zacieniowany obszar składa się z kwadratu $KLMN$ i czterech odcinków koła o promieniu $1$ i każdy z tych odcinków oparty na łuku odpowiadającym kątowi środkowemu o mierze $30^\circ$.
Pole odcinka koła $ML$ jest równe różnicy między polem wycinka koła $LAM$ i polem trójkąta $LAM$.
Pole wycinka koła równe jest $\frac{\pi}{12}$.
Rozpatrzmy trójkąt $LAM$. Wysokość $MP$ opuszczona na bok $AL$ równa jest połowie długości odcinka $MB$ i wynosi $\frac{1}{2}$, stąd pole trójkąta równe jest $\frac{1}{4}$
Pole odcinka $P_{ML} = \frac{\pi}{12} - \frac{1}{4}$
$|MP| = \frac{1}{2}$
$|AP| = \frac{\sqrt{3}}{2}$
$|PL| = 1 - \frac{\sqrt{3}}{2}$
$|ML|^2 = |PL|^2 + |MP|^2 = 2 - \sqrt{3}$
Pole rozważanej figury równe jest sumie pola kwadratu o boku $ML$ i czterech pól odcinków kół opartych na cięciwach $ML, MN, NK, KL$.
$P_{MNKL} = \frac{\pi}{3} + 1 - \sqrt{3}$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>