Zbiór zadań, (zadania różne)
Zadanie 304
Na okręgu o środku $O$ zaznaczono punkty $A, B, C$ takie, że cięciwa $AB$ ma długość $12$, a cięciwa $BC$ jest równoległa do stycznej poprowadzonej w punkcie $A$ i odległa od tej stycznej o $4$. Oblicz pole trójkąta $BOC$.
Rozwiązanie
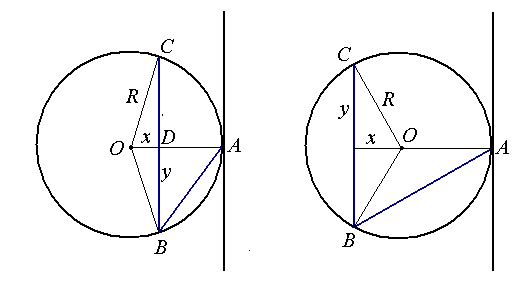
Należy rozpatrzyć dwa przypadki ze względu na położenie cięciwy $BC$
1. Z twierdzenia Pitagorasa dla trójkąta $ADB$ mamy $y^2 = 144 -16 = 128$
Z twierdzenia Pitagorasa dla trójkąta $ODB$ mamy $x^2 = 128 + R^2$
Dla $R = x+ 4$, mamy $x^2 + 128 = x^2 + 8x + 16$, skąd $x = 14$, $R=18$
Pole trójkąta $BOC$ równe jest $\frac{1}{2} \cdot 14 \cdot 2\sqrt{8} \approx 158.39$.
2. W przypadku drugim otrzymujemy układ równań:
$x^2+128 =R^2$
$x + R = 4$
Stąd $x^2 + 128 = x^2-8x + 16$, skąd $x<0$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>