Zbiór zadań, (zadania różne)
Zadanie 311
Ile nieprzystających trójkątów można utworzyć na wierzchołkach dwudziestokąta foremnego?
Rozwiązanie
Niech będzie dany $n$-kąt foremny. Opiszmy na nim okrąg.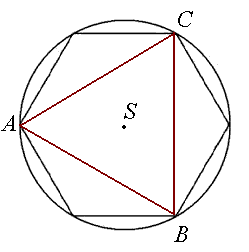
Możemy założyć, że jeden z wierzchołków trójkąta $ABC$, jest wierzchołkiem każdego z poszukiwanych trójkątów, ponieważ każdy trójkąt można obrócić wokół środka $S$.
Z twierdzenia o kącie środkowym i wpisanym wynika, ze każdy z kątów trójkąta jest wielokrotnością kąta $\alpha = \frac{360}{2n}$. Kąty przy wierzchołkach $A,B, C$ oznaczmy odpowiednio przez $a\alpha, b\alpha, c\alpha$.
Stąd $(a+b+c)\alpha = 180$, skąd $a+b+c = n$, gdzie $a,b,c \in [1,n-2]$
Każdy trójkąt wyznacza podział liczby $n$ na sumę trzech dodatnich całkowitych składników. Każdy taki podział wyznacza jeden z trójkątów i różnym podziałom odpowiadają nieprzystające trójkąty.
Dla $n=20$ otrzymujemy $33$ podziały na sumę trzech składników:
$1 + 1 + 18$
$1 + 2 + 17$
$1 + 3 + 16$
$1 + 4 + 15$
$1 + 5 + 14$
$1 + 6 + 13$
$1 + 7 + 12$
$1 + 8 + 11$
$1 + 9 + 10$
$2 + 2 + 16$
$2 + 3 + 15$
$2 + 4 + 14$
$2 + 5 + 13$
$2 + 6 + 12$
$2 + 7 + 11$
$2 + 8 + 10$
$2 + 9 + 9$
$3 + 3 + 14$
$3 + 4 + 13$
$3 + 5 + 12$
$3 + 6 + 11$
$3 + 7 + 10$
$3 + 8 + 9$
$4 + 4 + 12$
$4 + 5 + 11$
$4 + 6 + 10$
$4 + 7 + 9$
$4 + 8 + 8$
$5 + 5 + 10$
$5 + 6 + 9$
$5 + 7 + 8$
$6 + 6 + 8$
$6 + 7 + 7$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>