Zbiór zadań, (zadania różne)
Zadanie 313
Jakie jest prawdopodobieństwo, że trzy losowo obrane punkty na płaszczyźnie będą wierzchołkami trójkąta rozwartokątnego?
Rozwiązanie
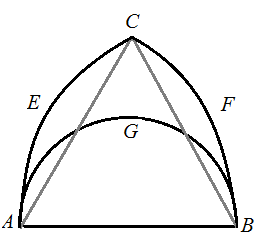
Przyjmijmy najdłuższy bok trójkąta jako $AB$, na boku tym poprowadźmy półokrąg $AGB$.
Z punktów $A$ i $B$ prowadzimy dwa łuki $BFC$ oraz $AEC$ o promieniu długości $|AB|$ i przecinające się w punkcie $C$.
Wówczas trzeci wierzchołek trójkąta nie może znajdować się poza figurą ograniczoną $ABFCE$
Jeśli trzeci wierzchołek leży wewnątrz półkola, to trójkąt jest rozwartokątny, jeśli poza nim, to ostrokątny. Prawdopodobieństwo, że leży dokładnie na półokręgu lub odcinku $AB$ równe jest prawie zero.
Stąd szukane prawdopodobieństwo równe jest stosunkowi powierzchni półkola i powierzchni figury ograniczonej $ABFCE$.
Załóżmy że $AB = 2a$, wówczas powierzchnia półkola równa jest $\frac{\pi a^2}{2}$, a powierzchnia figury ograniczonej $ABFCE$ równa jest $2\frac{4\pi a^2}{6}- a^2\sqrt{3} = a^2(\frac{4\pi}{3} - \sqrt{3})$
Prawdopodobieństwo równe jest $\frac{\frac{\pi}{2}}{\frac{4}{3}\pi - \sqrt{3}} = \frac{3}{8 - \frac{6\sqrt{3}}{\pi}} \approx 0.639$
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>