Zbiór zadań, (zadania różne)
Zadanie 317
Dany jest trójkąt równoramienny o podstawie $a$, ramionach $b$, wysokości $h$ i kącie między ramionami $\alpha$. Dla jakiej największej całkowitej miary (w stopniach) kąta $\alpha$, można zbudować trójkąt złożony z odcinków $a, b, h$?
Rozwiązanie
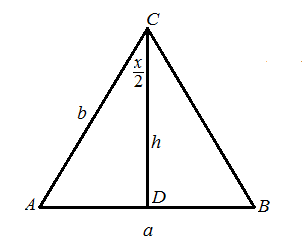
Warunkiem koniecznym i dostatecznym istnienia trójkąta o bokach $a, b, h$ jest aby, spełniona była nierówność trójkąta $b+h >a$. Dwie pozostałe nierówności $b+a>h$ oraz $a+h>b$ będą zawsze spełnione.
Z trójkąta $ADC$ mamy $h=b\cos{\frac{x}{2}}$ oraz $\frac{a}{2} = b\sin{\frac{x}{2}}$.
Podstawiając do nierówności $b+h >a$ otrzymujemy:
$b (1+\cos{\frac{x}{2}}) > 2b\sin{\frac{x}{2}}$
$1+\cos{\frac{x}{2}} > 2\sin{\frac{x}{2}}$
lub $2\cos^2{\frac{x}{4}} > 4\sin{\frac{x}{4}}\cos{\frac{x}{4}}$
Ponieważ $\frac{x}{4}$ jest kątem ostrym, więc $\frac{1}{2} > tg{\frac{x}{4}}$.
$x < 4 arctg{\frac{1}{2}}$
Ponieważ $4 arctg{\frac{1}{2}}$ to więcej niż $106^\circ$ a mniej niż $107^\circ$, więc rozwiązaniem jest $\alpha=106^\circ$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>