Zbiór zadań, (zadania różne)
Zadanie 333
Oblicz powierzchnię obszaru zdefiniowanego przez $x^2 + y^2 \le |x| + |y|$ w $R^2$.
Rozwiązanie
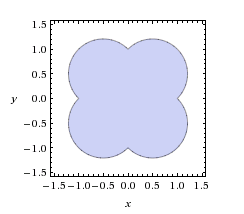
Rozpatrzmy obszar należący do pierwszej ćwiartki. Powierzchnia całego obszaru będzie czterokrotnie większa.
W pierwszej ćwiartce otrzymujemy $x^2 + y^2 \le x + y \Rightarrow (x - \frac{1}{2})^2 + (y - \frac{1}{2})^2 \le \frac{1}{2}$. Nierówność opisuje koło o promieniu $r=\frac{\sqrt{2}}{2}$ i środku w punkcie $(\frac{1}{2}, \frac{1}{2})$. Obszar znajdujący się w pierwszej ćwiartce to suma obszaru półkola o promieniu $r$ i trójkąta prostokątnego równoramiennego o przyprostokątnej długości $1$. Powierzchnia ta równa jest $\frac{1}{2} + \frac{\pi}{4}$. Powierzchnia całego obszaru równa jest $2 + \pi$.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>