Zbiór zadań, (zadania różne)
Zadanie 6
W trójkącie prostokątnym ABC przedłużono przeciwprostokątną AB i odłożono odcinek AD równy AC oraz odcinek BE równy BC. Jaką miarę ma kąt DCE?
Rozwiązanie
Rysunek do zadania.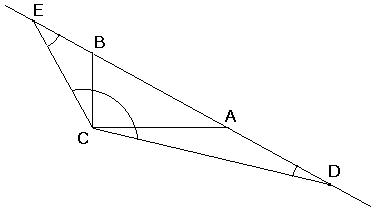
Trójkąt BEC oraz trójkąt ACD to trójkąty równoramienne, zatem kąt BEC i kąt BCE mają równe miary, oraz kąt ADC i kąt ACD także mają równe miary.
Miara kąta ACB równa jest oczywiście 90°.
Aby obliczyć miarę kąta DCE, należy do kąta prostego dodać sumę miar kątów α i β z rysunku powyżej.
Rozpatrzmy trójkąt DCE.
α + α + 90° + β + β = 180°
2α + 2β = 90°
2(α + β) = 90°
α + β = 45°
Miara kąta DCE rowńa jest zatem: 45° + 90° = 135°
Odp. Miara kąta DCE równa jest 135°.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>