Zbiór zadań, (zadania różne)
Zadanie 91
Przekątna czworokąta dzieli go na dwa trójkąty, których obwody wynoszą 25 i 27. Oblicz długość tej przekątnej, jeżeli obwód tego czworokąta jest równy 32.
Rozwiązanie
Niech obwody trójkątów ABD i BCD będą równe 25 i 27.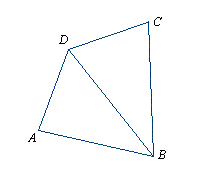
Suma obwodów tych trójkątów jest równa obwodowi czworokąta ABCD i podwójnej długości przekątnej BD. Zatem 25 + 27 = Ob(ABCD) + 2|BD|. Stąd |BD| = 10.
powrót do zbioru zadań | wersja do druku << poprzednie zadanie następne zadanie >>