Symetria
Symetria osiowa
Symetrią osiową względem prostej k nazywamy przekształcenie płaszczyzny, w którym każdemu punktowi A przyporządkowany jest punkt A', leżący na prostej prostopadłej do tej prostej k przechodzącej przez punkt A w tej samej odległości od k co punkt A, ale po drugiej stronie prostej k. Prostą k nazywamy osią symetrii.
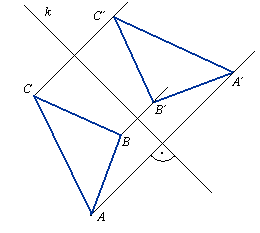
Symetrię osiową względem prostej k nazywamy również odbiciem symetrycznym względem
prostej k lub symetrią względem prostej k.
Każdy punkt prostej k jest punktem stałym symetrii.
Symetria środkowa
Symetrią środkową względem punktu O zwanego środkiem symetrii nazywamy przekształcenie płaszczyzny, w którym punkt O jest stały, a każdemu innemu punktowi A przyporządkowuje punkt A' taki, że punkt O jest środkiem odcinka AA'.
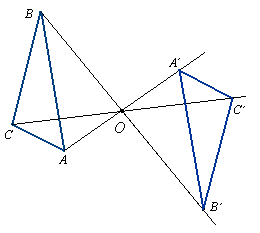
Symetrię środkową o środku O nazywamy również odbiciem symetrycznym względem punktu O
lub symetrią względem punktu O.
Punkt O jest punktem stałym symetrii środkowej.
Figura f ma środek symetrii S, jeżeli punkty symetryczne względem S do punktów figury
f też należą do f. Punkt S nazywamy środkiem symetrii figury f.
Oś symetrii figury
Figura f ma oś symetrii k, jeżeli punkty symetryczne względem k do punktów figury f też należą do f. Prostą k nazywamy osią symetrii figury f.
Figurę, która posiada co najmniej jedną oś symetrii nazywamy osiowosymetryczną.
Posiadanie osi symetrii wśród wielokątów:
trójkąt równoramienny - 1 oś symetrii,
trójkąt równoboczny - 3 osie symetrii,
kwadrat - 4 osie symetrii,
prostokąt - 2 osie symetrii,
romb - 2 osie symetrii,
równoległobok - nie posiada osi symetrii
trapez równoramienny - 1 oś symetrii,
deltoid - 1 oś symetrii.