System babiloński

Babilońskich znaków używano w Mezopotamii około 5000 lat temu, zachowały się do naszych czasów na glinianych tabliczkach. Wśród tych tabliczek znaleziono sporo takich, na których wypisana jest pewna wiedza matematyczna Babilonii. Babilończycy pisali pismem klinowym. Liter klinowych było dużo, ale znaków cyfrowych było niewiele. Babilończycy, którzy byli sławni za swoje słynne obserwacje astronomiczne i obliczenia, korzystali z pozycyjnego systemu sześćdziesiątkowego (systemu liczbowego o podstawie 60), który towarzyszy nam jeszcze dziś. Do dzisiaj dzielimy godziny na sześćdziesiąt minut, minuty na sześćdziesiąt sekund.

System babiloński może wydawać się skomplikowany, jednak w rzeczywistości Babilończycy potrzebowali tylko dwóch symboli - dla oznaczenia jedności i dziesiątek. Znak 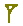jeden oznaczał jedności, znak dziesięc oznaczał dziesiątki. Ich cyfry były zbudowane właśnie z tych dwóch znaków.

1	2	3	4	5	6	7	8	9	10

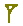Kolejny znak 11 był połączeniem znaku 10 i 1: 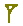i tak aż do 60.

Zapis liczby całkowitej w systemie babilońskim ma postać:
a_i-1a_i-2 ... a₂ a₁ a₀ = a_i-1 · 60^i-1 + a_i-2 · 60^i-2 + ... + a₂ · 60² + a₁ · 60¹ + a₀ · 60⁰

Chociaż sześćdziesiąt może wydawać się dużą liczbą jak na podstawę, to jednak są pewne tego korzyści. Sześćdziesiąt jest najmniejszą liczbą, która dzieli się bez reszty przez dwa, trzy, cztery, pięć i sześć. Można ją podzielić również przez dziesięć, dwanaście, piętnaście, dwadzieścia i trzydzieści.

Problem sprawia tylko brak cyfry na określonej pozycji. Babilończycy nie znali cyfry zero. Zamiast zera pozostawiali na danej pozycji puste miejsce. Problem pojawiał się wtedy, gdy obok siebie było kilka takich pustych miejsc. Jednak w rachunkach starożytności nie operowano olbrzymimi wartościami, więc puste miejsca obok siebie w zapisie babilońskim były raczej rzadkością. W późniejszym okresie zaczęto takie puste miejsca zaznaczać małą, pionową kreseczką umieszczoną u góry.