Wklęsłość i wypukłość krzywej
Wykres funkcji y = f(x) różniczkowalnej w punkcie x0 nazywamy wypukłym (wklęsłym) w tym punkcie, jeżeli istnieje takie sąsiedztwo S punktu x0, że dla każdego x∈S punkt P = (x, f(x)) wykresu leży powyżej (poniżej) stycznej poprowadzonej do wykresu w punkcie o odciętej x0.
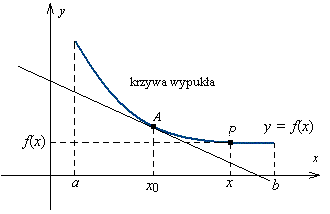
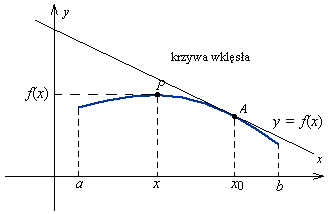
Wykres funkcji y = f(x) wypukły (wklęsły) w każdym punkcie x∈(a, b) nazywamy wypukłym (wklęsłym) w przedziale (a, b).
Jeżeli f ''(x0) < 0 dla każdego x∈(a, b), to wykres funkcji f jest wklęsły w przedziale (a, b).
Jeżeli f ''(x0) > 0 dla każdego x∈(a, b), to wykres funkcji f jest wypukły w przedziale (a, b).
Punkt P = (x0, f(x0), gdzie
x0∈(a, b), nazywamy punktem przegięcia wykresu funkcji f,
jeżeli wykres ten jest:
- wklęsły w sąsiedztwie S-(x0, δ)
i wypukły w sąsiedztwie S+(x0, δ) lub
- wypukły w sąsiedztwie S-(x0, δ)
i wklęsły w sąsiedztwie S+(x0, δ).
Warunkiem koniecznym na to, aby punkt P = (x0, f(x0)
był punktem przegięcia wykresu funkcji f jest f ''(x0) = 0,
warunkiem wystarczającym zaś jest
f ''(x) < 0 dla x < x0
f ''(x) > 0 dla x > x0
albo
f ''(x) > 0 dla x < x0
f ''(x) < 0 dla x > x0
Jeżeli funkcja f spełnia następujące założenia:
ma w pewnym otoczeniu punktu x0 pochodne trzeciego rzędu włącznie,
f(3)(x) jest ciągła w x0,
f ''(x0) = 0 i f(3)(x0) ≠ 0,
to punkt x0 jest punktem przegięcia wykresu funkcji f.